In this article, you are going to know the complete description of the branches of science.
From your childhood, you may probably hear many terms combining with the “science” word. So, sometimes you may think about this study area as an uncategorized subject. But it is wrong. We can scientifically categorize this board study area for our learning purpose.
After reading this article, you can prove that no one can be an expert in all of the science subject areas. But don’t get a negative feeling. All of these sub-subject areas combined with each other. That’s mean the basic knowledge of one subject area is needed for all of the other subject areas’ applications. So your preferred area should be a diamond. Finally, we’ll discuss more about this.
What you can learn from this article
- The main branches of science
- What are The Natural Sciences?
- What are the Formal Sciences?
- What are the Social Sciences?
- What are The Applied Sciences?
- Overlapping Science Subject areas.
- Branches of Science Complete Summary

The main branches of science
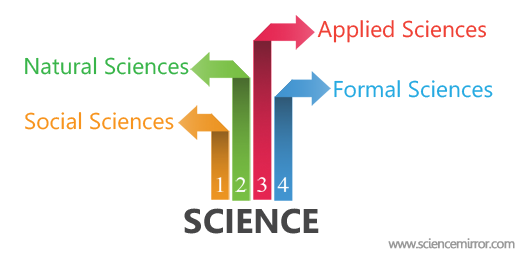
Mainly Science is divided into four main branches. They are,
- Natural Sciences
- Social Sciences
- Formal Sciences
- Applied Sciences
Each of these branches has sub-branches according to the nature of the subject. And also, there are overlapping science subjects. These subjects build with two sub-branches of the above main subject areas.
The Formal Sciences act as a tool for both Natural and Social Sciences to build the applied science area. As I mentioned above, all of these areas are bound with each other.
If you are a student you may study about biology, Chemistry and Physics under the name of science subject. So, Sometime you may say these three subjects are the main branches of science. But these three study areas are only sub-branches of the natural sciences. All of the general people indeed see science through only these three main windows. But when we consider all of the studies, it can identify these four major categories.
If you are going to talk about only about chemistry, biology, and physics. You have to divide these three gems under Life science and Physical science, sub-branches of natural sciences. Next, let’s see about this main subject.
What are The Natural Sciences?
Do you want to learn about the universe? Or the nature? Then, this is your major study area.
Explain the various rules of the nature by using the scientific method known as the natural sciences.
Scientists observe their environment and identify a specific problem or get a problem from the day to day that bonded with the nature. Then they are apply the scientific method to find the solution or explain the problem. The scientific method is the main procedure for do a standard research.
As I mentioned earlier the natural sciences are divided into two main branches,
- Physical science
- Life Science
What are the physical Sciences?
The Physical Science is an important branch of science. If we consider all branches of Science the physical science can introduce as the platinum subject area. Becourse the knowledge of this subject area is a very important one for other all subjects’ areas also. Even social sciences.
Subject areas of physical sciences,
This valuable science subject area has four sub subject areas they are,
- Physics
- Chemistry
- Space Science
- Earth Science
All science lovers know the value about these subjects. Actually the modern technical world totally depends on the explanation of the Physics.
The transistors are invented through the theories of the physics. What the electricians are do, they combine this transistors with logics and make a useful application for the human. Like this we can explain the importance of these subjects.
Let’s see the each of these subjects.
The Science of matter, Chemistry.
Chemistry is the study of matter and its changes with different conditions. But someone can Argive the physics also says about the matter. But chemistry studies deeply about the matter. The matters that found on earth can be categorized into organic and inorganic materials. And also, all matters are made up of atoms. For study these matters there are three main branches of chemistry,
- Organic Chemistry
- Inorganic chemistry
- Nuclear Chemistry
Organic chemistry chemists study about carbon-based matters and make affordable applications to the world. Other all matters on the earth study through the inorganic chemistry.
The nuclear chemistry subject provides you the knowledge of the atom. Such as structure, energy changes, and other all physical phenomenons combines with the atomic level.
These main chemistry subjects also include overlapping sub-branches. For example, organometallic chemistry is the study area of the matters that made up of carbon and transition metals.
The science of systems, Physics
Physics can be used to describe all non-living and living systems. It can describe how the system is placed on the space, the motion of the system, and other physical properties.
There are two types of study areas of physics. Classical physics and quantum physics. Classical physics also known as the Newtonian Physics. Because it is based on newton’s laws. After introducing the scientist mask plank’s quantum theory and contribution of the scientist Albert Instain’s knowledge, quantum physics start to develop as a subject.
The study area of the nano-level of the matter is known as nanoscience. Nanoscience is studied under both chemistry and physics.
The science of space, Space Science.
It is don’t matter if you are don’t love science words but. Even a child also like to know about the space. Specially planets, stars, black holes, etc. the study about these things known as astronomy. Under astronomy, in brief, we can say its study about the visible space.
The study area about the whole universe known as cosmology. Another interesting and endless subject area.
The science of our living planet, Earth Science.
There are a lot of curious things in the earth to study. The study area about the lithosphere is known as the geology. And the study area of hydrosphere atmosphere and biosphere includes under the ecology subject area.
I think all of the physical things that we know can include in one of the above sections discussed under physical science. Also, it is vital to distinguish the differences between physics and physical science.
What is Life Science?
“The Life” there is no exact definition for this phase. Scientists give only the characteristics when describing the life. So, there are a lot of things to study in the living word. All living things are studied under life science or known as biology. In life science, there are three main branches
- Zoology
- Botany
- Molecular Biology
Love animals? Then zoology is your subject. In zoology it is study about the large kingdom of animals deeply
Or
Love plants? Then you are a Botanist. Study deeply about the kingdom of the plant known as the Botany.
The tool of life science known as molecular biology. In molecular biology, study about the molecular level of all living things. Likes biomolecules, metabolism pathways, etc.
What are the Formal Sciences?
The difference between natural science and formal science is, at formal science, all theories are not going to prove with the real word like natural sciences. All theories in formal science come with human imaginations. Let’s see the major areas of formal science.
- Mathematics
- Logic
- Statistics
- Decisions
All of the above sciences are need to be study under the care and according to a system. For this, mathematics can be used as a tool.
For study about the most intelligent activities, the Logic is used. Therefore this subject area is used for computer science as a tool.
All scientific researches need the statistics as a tool to organize and analyze the data and results of the study.
Subjects like economics, philosophy study under the decisions.
What are the Social Sciences?
Want to study law, History, the relationship among humans, languages like subjects? Then you have to collect knowledge under the social sciences. After the development of the technology, the study through social science is getting easier due to social networks.
What are The Applied Sciences?
All the other three science branches study about the theory of the particular subjects. By knowing only about the theories of a specific subject, it’s hard to have the benefits of that subject. Therefore the applied science area came into the science subjects.
In applied science it is study about how to theories of a subject apply for the humans’ applications. Such as making inexpensive fuels for energy requirements.
This branch is a significant branch of science. Because we want an application from science rather than knowing the theories. All of the industrial applications come with applied sciences studies. Also, all of the science subjects have an applied science area, for example, applied physics, applied mathematics, Applied Biology, etc.
Overlapping Science Subject areas.
When we consider all of the different science subject areas. It can introduce a new study area by combining two of these science subjects. Look about the following examples.
Biochemistry
The combination of Biology and Chemistry make a new study area known as the Biochemistry.
Geophysics
The Combination of the Gelogogy and Physices sub subjects areas makes the geophysics subject
Biostatistics.
The biology from natural sciences and statistics as a tool from formal sciences can be combined and then known as bio statistics.
Astronomy.
Study the life of outer the earth known as astrobiology. Astronomy comes from space sciences, and biology comes from the natural sciences.
Environmental Science
This is an interdisciplinary study filed. For expertise in environmental science you need to gain knowledge in Chemistry, Biology, Physics and even in Geology. Sometimes you will need social science knowledge to answer the questions in environmental science.
Like this Human can make a lot of studying areas by combining science subjects.
Branches Of Science Complete Summary
The Board area of science can be categorized according to the following table with four main branches.
| Branches of Science | |||
|---|---|---|---|
| Natural Science | Formal Science | Social Science | Applied Science |
|
|
|
|


Thanks a lot for providing information on science topic